8550. Печать
шахматной доски
Задана шахматная доска
размера n * n. Она заполнена числами от 1 до n2 следующим образом: первые ceil(n2 / 2) чисел от 1 до ceil(n2 / 2) записаны в
ячейках с четной суммой координат слева направо и сверху вниз. Остальные n2 – ceil(n2 / 2) чисел от ceil(n2 / 2) + 1 до n2 записаны в ячейках с
нечетной суммой координат слева направо сверху вниз.
Операция ceil(x / y) означает деление x на y округленное вверх.
Вход. Одно
целое число n (1 ≤ n ≤ 9).
Выход. Выведите матрицу – шахматную
доску в описанном выше виде. Следите за выравниванием.
|
Пример входа 1 |
Пример выхода 1 |
|
5 |
1 14 2 15
3 16 4 17
5 18 6 19
7 20 8 21 9 22 10 23 11 24 12 25 13 |
|
|
|
|
Пример входа 2 |
Пример выхода 2 |
|
6 |
1 19 2 20
3 21 22 4 23
5 24 6 7 25
8 26 9 27 28 10 29 11
30 12 13 31 14 32
15 33 34 16 35 17
36 18 |
РЕШЕНИЕ
массив
Анализ алгоритма
Пронумеруем
строки и столбцы шахматной доски от 1 до n.
Установим счетчик cnt = 1. Будем перебирать ячейки результирующей двумерной
таблицы n * n. Каждой
ячейке с четной суммой координат присваиваем значение cnt и после каждого
присваивания увеличиваем cnt на 1. Затем снова переберем ячейки результирующей таблицы и
аналогично заполним ячейки с нечетной суммой координат.
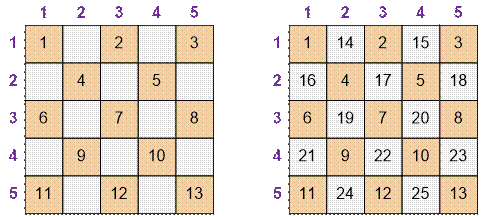
Пример
Рассмотрим
первый пример, для которого n = 5.
Слева приведен
первый проход по двумерному массиву – заполнение ячеек с четной суммой
координат. Справа показан второй проход – заполнение ячеек с нечетной суммой
координат.
Реализация алгоритма
Объявим двумерный
массив.
#define MAX 110
int m[MAX][MAX];
Читаем значение n.
scanf("%d", &n);
Первые ceil(n2 / 2)
чисел от 1 до ceil(n2 / 2)
заносим в ячейки с четной суммой координат.
cnt = 1;
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
if ((i + j) % 2
== 0) m[i][j] = cnt++;
Остальные n2 –
ceil(n2 / 2) чисел
от ceil(n2 / 2)
+ 1 до n2 заносим в ячейки
с нечетной суммой координат.
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
if ((i + j) % 2
== 1) m[i][j] = cnt++;
Выводим двумерную матрицу.
for (i = 1; i <= n; i++)
{
for (j = 1; j
<= n; j++)
printf("%2d
", m[i][j]);
printf("\n");
}